Прямокутний паралелепіпед — це одна з найважливіших геометричних фігур, яку учні вивчають у школі. Він зустрічається у повсякденному житті, у будівництві, архітектурі, а також у фізиці та математиці. Тому важливо зрозуміти його властивості, навчитися обчислювати площу та об’єм і правильно застосовувати знання у практиці.
Що таке прямокутний паралелепіпед
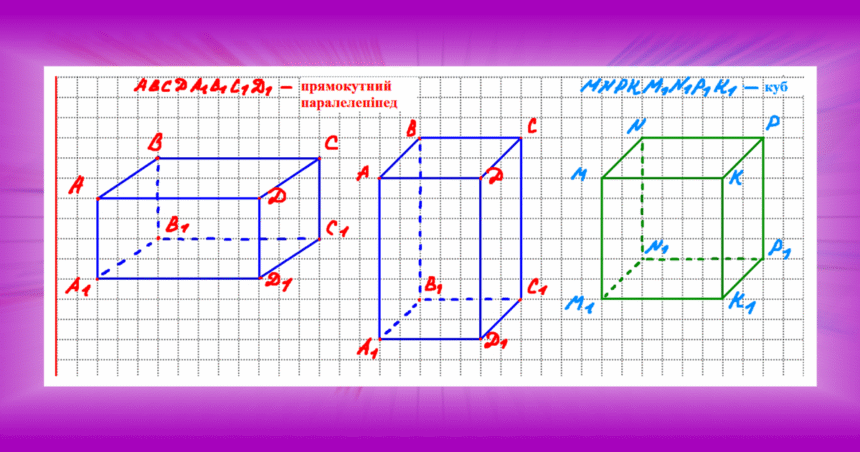
Прямокутний паралелепіпед — це геометричне тіло, яке має шість граней, і кожна з них є прямокутником. У нього є вісім вершин і дванадцять ребер. Важливо зазначити, що всі грані цього тіла попарно паралельні.
Властивості прямокутного паралелепіпеда
Прямокутний паралелепіпед має кілька властивостей, які роблять його унікальним. По-перше, протилежні грані рівні та паралельні. По-друге, всі кути між сусідніми гранями дорівнюють 90 градусів. Крім того, діагоналі цього тіла мають однакову довжину, що є ключовою рисою фігури.
Формули для обчислень

Щоб працювати з прямокутним паралелепіпедом, потрібно знати кілька базових формул.
Формула об’єму прямокутного паралелепіпеда
Об’єм VVV обчислюється за формулою:
V=a⋅b⋅cV = a \cdot b \cdot cV=a⋅b⋅c
де aaa, bbb, ccc — довжини трьох вимірів.
Формула площі поверхні прямокутного паралелепіпеда
Площа поверхні SSS визначається так:
S=2(ab+bc+ac)S = 2(ab + bc + ac)S=2(ab+bc+ac)
де aaa, bbb, ccc — довжини ребер.
Приклади задач з прямокутним паралелепіпедом
Розглянемо кілька прикладів, які допоможуть краще зрозуміти тему.
Приклад 1
Знайти об’єм прямокутного паралелепіпеда з ребрами 3 см, 4 см і 5 см.
V=3⋅4⋅5=60 см3V = 3 \cdot 4 \cdot 5 = 60 \, см^3V=3⋅4⋅5=60см3
Приклад 2
Обчисліть площу поверхні прямокутного паралелепіпеда з ребрами 2 см, 3 см і 4 см.
S=2(2⋅3+3⋅4+2⋅4)=2(6+12+8)=52 см2S = 2(2 \cdot 3 + 3 \cdot 4 + 2 \cdot 4) = 2(6 + 12 + 8) = 52 \, см^2S=2(2⋅3+3⋅4+2⋅4)=2(6+12+8)=52см2
Використання прямокутного паралелепіпеда у житті

Прямокутний паралелепіпедд не є лише абстрактною фігурою з підручника. Ми бачимо його у коробках, шафах, цеглинах, книжках. Тобто, кожен день ми маємо справу з предметами, які мають форму прямокутного паралелепіпеда. Тому його вивчення допомагає краще орієнтуватися у просторі та розвивати логічне мислення.
Прямокутний паралелепіпед у шкільній програмі
У школі вивчення прямокутного паралелепіпеда починається у середніх класах. Учні дізнаються про його визначення, властивості, навчаються обчислювати площу поверхні та об’єм. Згодом ці знання застосовуються під час розв’язування складніших задач з геометрії, алгебри та фізики.
Переваги знань про прямокутний паралелепіпед
Вивчення цієї фігури допомагає не лише скласти іспити з математики, а й практично застосовувати знання. Наприклад, розрахунок кількості матеріалів для будівництва чи пакування товарів неможливий без вміння працювати з поняттям прямокутного паралелепіпеда.
Часті помилки учнів
Учні часто плутають прямокутний паралелепіпед із кубом. Важливо пам’ятати, що куб — це особливий випадок, коли всі ребра рівні. Інша типова помилка — неправильне підставлення даних у формули. Тому потрібно завжди уважно перевіряти розрахунки.
Читати далі: Омоніми – приклади, значення та роль у мові – повний гід
FAQ: поширені питання про прямокутний паралелепіпед
Це геометричне тіло з шістьма прямокутними гранями, дванадцятьма ребрами і вісьмома вершинами.
Об’єм дорівнює добутку довжин трьох вимірів: V=a⋅b⋅cV = a \cdot b \cdot cV=a⋅b⋅c.
Куб — це прямокутний паралелепіпед, у якого всі ребра однакові.
Формула: S=2(ab+bc+ac)S = 2(ab + bc + ac)S=2(ab+bc+ac).
У будівництві, дизайні, пакуванні, архітектурі, фізиці та повсякденних предметах.